Modified Robust Adaptive Process Control with Improved Transient Performance and Its Application to Atmospheric Plasma Spray Process

Abstract

This chapter presents the $\sigma$-modification and the low-frequency learning to the model reference adaptive control (MRAC) to improve the transient performance of a closed-loop control system under uncertainties and external disturbances. The $\sigma$-modification improved the robustness to external bounded disturbances, and the low-frequency learning enabled fast adaption without creating high-frequency oscillations. The feasibility of the resulting robust adaptive control architecture is tested for the atmospheric plasma spray process (APSP) to achieve consistency in ceramic coatings through numerical simulations. The robustness and adaptability of the modified and the standard MRAC architecture are investigated under artificially induced disturbances. The proposed architecture shows better performance than the standard MRAC under external disturbances. The results depict the improved transient performance with faster convergence and smooth variations in closed-loop control signals without creating high-frequency oscillations or steady-state errors.

1. Introduction

Adaptive control is a popular control methodology for various applications due to its unique ability to accommodate system parametric and structural uncertainties caused by payload variations, component failures, and external disturbances [1]. The model reference adaptive control (MRAC) is a well-known adaptive control approach. The controller gains of the MRAC are updated based on the tracking error between the measured outputs of the uncertain system with outputs of the selected reference model such that these gains force the uncertain system to track the reference model adaptively. In many applications, the MRAC performs satisfactorily and achieves asymptotic system performance without excessive reliance on the system models [2]. However, it suffers the lack of robustness properties in the presence of model uncertainty and external disturbances, which result in various instabilities, such as parameter drifts, high-gain instability, instability resulting from fast adaption, and high-frequency instability [3, 4, 5].

For improving the robustness and transient performance and avoiding high-frequency instability in the presence of uncertainties and external disturbances, a significant research effort has been carried out by modifying the adaptive laws of the MRAC and its architecture [6]. First, to improve the robustness, many researchers have proposed various robust MRAC (we referred to as R-MRAC) schemes by modifying the adaptive laws of the MRAC. The R-MRAC using fixed modification [5] achieves the desired robustness and performance without explicit knowledge of plant dynamics and bounds of the external disturbances. The modified MRAC achieves the boundedness of the closed-loop signals; however, the asymptotic convergence of the tracking error in the absence of the disturbances is not achievable. Apart from this, the MRAC and the R-MRAC using modification schemes can create high-frequency oscillations in control responses when the fast adaption using the high adaptive gains is enabled; thus, it leads to process instability. Additionally, the fixed modification can create a steady-state error and often may lead to a bursting phenomenon [5]. Yucelen and Haddad have proposed low-frequency learning to the MRAC to avoid high-frequency oscillation in control responses in the presence of high adaptive gains [2]. In their work, it was implemented to a nonlinear uncertain plant dynamic without a disturbance term. The fast adaption is achieved using high-adaptive gains by filtering out the high-frequency content in the control responses. This scheme preserves the ideal property of the MRAC, that is, the asymptotic convergence of the tracking error to zero in the absence of the disturbance term.

The motivation, then, is to develop a robust adaptive process control scheme with an improved transient performance by overcoming the issues related to the MRAC. This chapter presents a modified robust model reference adaptive control (we call it MR-MRAC) architecture by incorporating two modifications to the MRAC. First, to achieve robustness in the presence of bounded disturbances, the R-MRAC is considered by incorporating $\sigma$-modification to the MRAC. Next, to avoid steady-state error associated with $\sigma$-modification and to enable fast adaption using high-adaptive gain, we used low-frequency learning with low-pass filters for the gain estimations. The resulting MR-MRAC scheme achieves the boundedness of all responses of closed-loop control and convergence of the tracking error to a small bound in the presence of bounded disturbances. The feasibility of the MR-MRAC architecture is tested for the atmospheric plasma spray process (APSP), and its adaptability and robustness in the presence of external disturbances to achieve desired consistency in the outputs have been investigated.

The APSP has become one of the most efficient and reliable techniques to produce a wide variety of coatings, such as low porosity, thermal barrier, wear, and corrosive-resistant coatings, in different applications. The APSP is a common technique to produce ceramic coatings and is capable of producing functionally graded coatings (FGCs) [7]. Due to the demand for high-volume manufacturing of these coatings, reproducibility and repeatability of the coating quality are of prime importance.

As depicted in Figure 1, the APSP includes plasma generation, plasma and in-flight particle interaction, and deposit formation on a substrate. The plasma produced by the injection of Ar and H₂ into the torch exits from it at a very high temperature and speed. Powder particles injected into the plasma travel with it to the substrate and, upon impact, are deposited on it. The y- and the z-axes are, respectively, along and perpendicular to the plasma jet. Particles’ axial velocity and temperature are monitored in the 1-cm wide observation window located near the substrate to be coated. Complex interactions between plasma and particles significantly [9, 10], vary coating properties that affect the process repeatability [11]. Due to large velocity and temperature gradients in a plasma jet, even small changes in process parameters can significantly alter mean particles’ states (mean values of temperature, and axial velocity at the instant of striking the substrate), and thus the quality of the coatings [12]. Even with the operating parameters set constant during the process, the particles’ states before impacting the substrate can change over time due to noise variables such as nozzle wear, injector wear, pulsing of powder due to leaks, worn parts in the powder feeder, and powder dampness.

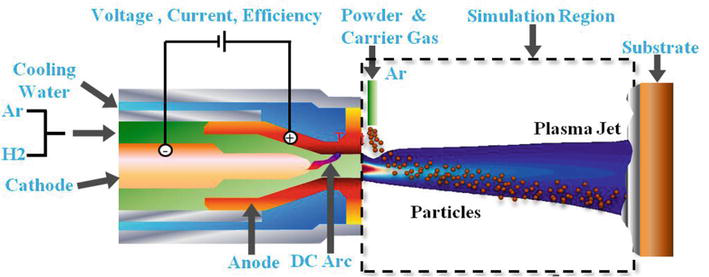
Figure 1.

Schematics of the APSP for producing ceramic coating using a single torch—Single injector system [8].

We presented the complete details of the design of the adaptive process control for APSP (validation of numerical simulations, screening of process parameters, finding optimal input parameters, system identification, and the control design) are given in Refs. [13] and [14] for ceramic coating using ZrO₂ powder with a single torch – single injector system and in Ref. [15] for FGCs using a mixture of the NiCrAlY and the ZrO₂ particles with a single torch – two injector system. This chapter discusses the proposed MR-MRAC architecture for generating ceramic coating using ZrO₂ powder. The control objective is to maintain the mean axial velocity and temperature of the particles collected in the observation window as the desired values within small bounds by attenuating the influence of external disturbances.

The remainder of this chapter is organized as follows. Section 2 presents preliminaries about the standard MRAC. Section 3 provides the proposed modified robust model reference adaptive control (MR-MRAC) and its stability properties for multi-inputs and multi-outputs (MIMO) linear time-invariant system with bounded external disturbances. The adaptive and robust performance of the proposed controller using numerical simulations for illustrative examples related to the APSP is presented in Section 4. Finally, the conclusions are summarized in Section 5.

2. MRAC problem formulation

We choose the following plant dynamics with $m$ inputs and $n$ outputs and inclusion of disturbance term:

$$\dot{y}\left(t\right)=\mathit{Ay}\left(t\right)+\mathit{Bu}\left(t\right)+d\left(t\right),y\left(0\right)=y_0$$E1

where $y\left(t\right)\in {\mathbb{R}}^n$ is the output vector, $u\left(t\right)\in {\mathbb{R}}^m$ is the control input vector, $A\in {\mathbb{R}}^{n\times n}$ and $B\in {\mathbb{R}}^{n\times m}$ are unknown constants and $A$ is Herwitz, $d\left(t\right)$ is the vector of unknown bounded smooth disturbances, which satisfies ${‖d\left(t\right)‖}_2\le d_{\mathit{max}},{‖\dot{d}\left(t\right)‖}_2\le {\dot{d}}_{\mathit{max}}$with unknowns and positive bounds $d_{\mathit{max}}\left(\ge 0\right),{\dot{d}}_{\mathit{max}}\left(\ge 0\right)$. The pair $\left(A,B\right)$ is assumed to be controllable, $y\left(t\right)$ is controllable, and $u\left(t\right)$ is measurable and locally bounded.

The reference model is described as follows:

$${\dot{y}}_m\left(t\right)=A_m{y}_m\left(t\right)+B_{m}r\left(t\right),y\left(0\right)=y_{m0}$$E2

where $y_m\left(t\right)\in {\mathbb{R}}^n$ is the reference model output vector, $r\left(t\right)\in {\mathbb{R}}^m$ is a bounded piecewise continuous reference input, $A_m\left(t\right)\in {\mathbb{R}}^{n\times n}$ is Hurwitz and $B_m\left(t\right)\in {\mathbb{R}}^{n\times m}$. The reference model and reference input $r\left(t\right)$ are chosen such that $y_m\left(t\right)$ represents a desired output trajectory that system output $y\left(t\right)$ must follow.

The objective is to design a control input $u\left(t\right)$ in Eq. (1) such that the closed loop system has bounded control signals and $y\left(t\right)$ adaptively tracks $y_m\left(t\right)$ with bounded errors in the presence of uncertainties. We assume there exist ideal gains $K^{\ast }\in {\mathbb{R}}^{m\times n}$ and $L^{\ast }\in {\mathbb{R}}^{m\times m}$ are chosen to satisfy the algebraic equations

$$A-B{K}^{\ast }=A_m,B{L}^{\ast }=B_m$$E3

If the matrices $A$ and $B$ are known, use the following controller:

$$u\left(t\right)=-K^{\ast }y\left(t\right)+L^{\ast }r\left(t\right)$$E4

In the absence of disturbance guarantees that $y\left(t\right)=y_m\left(t\right),\forall t\ge 0$ when $y\left(0\right)=y_m\left(0\right)$ or tracking error $\left|y\left(t\right)-y_m\left(t\right)\right|\to 0$ exponentially when $y\left(0\right)\ne y_m\left(0\right)$ for any bounded $r\left(t\right)$. Since the matrices $A\mathit{\text{and}}B$ are unknown, the ideal gain matrices $K^{\ast }\mathit{\text{and}}{L}^{\ast }$ are also unknown. Instead of using the ideal control law listed in Eq. (4), the following adaptive control law given by Eq. (5) is considered:

$$u\left(t\right)=-K\left(t\right)y\left(t\right)+L\left(t\right)r\left(t\right)$$E5

where $K\left(t\right)\in {\mathbb{R}}^{m\times n}\text{and}L\left(t\right)\in {\mathbb{R}}^{m\times m}$ are real-valued gain matrices and are the estimates of the ideal gains at time $t$. The following adaptive law of the MRAC scheme is used to calculate gains [5]:

$$\begin{array}{cc}\dot{K}\left(t\right)=\mathrm{\Lambda }{B}_m^T\stackrel{\sim }{P}e\left(t\right)y^T\left(t\right)\mathit{sgn}\left(l\right),& K\left(0\right)=K_0\\ \dot{L}\left(t\right)=-\mathrm{\Lambda }{B}_m^T\stackrel{\sim }{P}e\left(t\right)r^T\left(t\right)\mathit{sgn}\left(l\right),& L\left(0\right)=L_0\end{array}$$E6

Here, $\mathrm{\Lambda }={\mathrm{\Lambda }}^{\mathrm{T}}$ and $\stackrel{\sim }{P}={\stackrel{\sim }{P}}^T$ are $m\times m$ and $n\times n$ positive definite matrices, respectively. The matrix $P$ is the solution of the Lyapunov equation:

$$A_m^T\stackrel{\sim }{P}+\stackrel{\sim }{P}{A}_m+Q=0$$E7

For any $Q=Q^T>0$. For either positive or negative definite $L^{\ast }$, there exists a constant adaptive rate matrix $\mathrm{\Lambda }\in {\mathbb{R}}^{m\times m}$ such that ${\mathrm{\Lambda }}^{-1}=L^{\ast }\mathit{sgn}\left(l\right)$, where $l=1$ if $L^{\ast }$ is positive definite and $l=-1$ if $L^{\ast }$ is negative definite. The dynamics of the tracking error, $e\left(t\right)\equiv y\left(t\right)-y_m\left(t\right)$ can be written as:

$$\dot{e}\left(t\right)=A_{m}e\left(t\right)+B_m{L^{\ast }}^{-1}\left(-\stackrel{\sim }{K}\left(t\right)y\left(t\right)+\stackrel{\sim }{L}\left(t\right)r\left(t\right)\right)+d\left(t\right),e\left(0\right)=e_0$$E8

where $\stackrel{\sim }{K}\left(t\right)\triangleq K\left(t\right)-K^{\ast }$ and $\stackrel{\sim }{L}\left(t\right)\triangleq L\left(t\right)-L^{\ast }$ are parameter error.

Since $r\left(t\right)$ is bounded, this MRAC scheme can guarantee that the closed-loop signals are bounded and outputs of the reference model $y_m\left(t\right)$ asymptotically converge to the outputs $y\left(t\right)$ in the absence of external disturbance, that is, $d\left(t\right)=0$. If the adaption rate is increased to achieve faster convergence, the transient behavior of $y\left(t\right)$ and $u\left(t\right)$ cannot be guaranteed and lead to high-frequency oscillations in the closed-loop control signals [6].

3. Modified robust model reference adaptive control (MR-MRAC) formulation

The foregoing MRAC scheme may suffer from instabilities, such as parameter drift, high gains, and/or fast adaption [16]. Some of these could be avoided using the robust MRAC (R-MRAC) by modifying Eqs. (6)–(9) as proposed by Ioannou and Kokotovic [17].

$$\begin{array}{cc}\dot{K}\left(t\right)=\mathrm{\Lambda }\left(B_m^T\stackrel{\sim }{P}e\left(t\right)y^T\left(t\right)\mathit{sgn}\left(l\right)-\mathit{\sigma K}\left(t\right)\right),& K\left(0\right)=K_0\\ \dot{L}\left(t\right)=\mathrm{\Lambda }\left(-B_m^T\stackrel{\sim }{P}e\left(t\right)r^T\left(t\right)\mathit{sgn}\left(l\right)-\mathit{\sigma L}\left(t\right)\right),& L\left(0\right)=L_0\end{array}$$E9

To prevent the steady-state error due to the $\sigma$-modification and high-frequency oscillations in MRAC, we are using low-frequency learning with low-pass filters. We consider low-pass filters $K_f\left(t\right)\in {\mathbb{R}}^{m\times n}$, $L_f\left(t\right)\in {\mathbb{R}}^{m\times m}$ presented in Ref. [2], which are weight estimates of gains $K\left(t\right),L\left(t\right),$ respectively, and are given by

$$\begin{array}{cc}{\dot{K}}_f\left(t\right)=\lambda \left(K\left(t\right)-K_f\left(t\right)\right),& K_f\left(0\right)=K_0\\ {\dot{L}}_f\left(t\right)=\lambda \left(L\left(t\right)-L_f\left(t\right)\right),& L_f\left(0\right)=L_0\end{array}$$E10

where $\lambda >0$ is a design parameter that serves as the cutoff frequency to suppress the high-frequency oscillations in the closed-loop control system. These low-pass filters only pass gains with frequencies lower than that of cutoff values and the rest will be attenuated. Low-frequency learning is incorporated in $\sigma$-modified adaptive laws presented in Eq. (9) to enforce a distance criterion between the estimated gains $K\left(t\right),L\left(t\right)$ and estimated filter gains $K_f\left(t\right),L_f\left(t\right)$. This results in a minimization problem containing the following error criteria:

$$\begin{array}{c}\underset{K_f}{min}{J}_K\left(K,K_f\right)=\frac{1}{2}{‖K\left(t\right)-K_f\left(t\right)‖}_F^2\\ \underset{L_f}{min}{J}_L\left(L,L_f\right)=\frac{1}{2}{‖L\left(t\right)-L_f\left(t\right)‖}_F^2\end{array}$$E11

The negative gradient of the cost function with respect to gain direction leads to

$$-\frac{\partial J_K}{\partial K}=-\left(K\left(t\right)-K_f\left(t\right)\right);-\frac{\partial J_L}{\partial L}=-\left(L\left(t\right)-L_f\left(t\right)\right)$$E12

The implementation of the MR-MRAC to the APSP is the same as that of Refs. [14] and [18] except the following form of the adaptive law is used:

$$\begin{array}{cc}\dot{K}\left(t\right)=\mathrm{\Lambda }\left(B_m^T\stackrel{\sim }{P}e{y}^T-\sigma \left(K-K_f\right)\right),& K\left(0\right)=K_0\\ \dot{L}\left(t\right)=\mathrm{\Lambda }\left(-B_m^T\stackrel{\sim }{P}e{r}^T-\sigma \left(L-L_f\right)\right),& L\left(0\right)=L_0\end{array}$$E13

Define $e\left(t\right)\triangleq y\left(t\right)-y_m\left(t\right)$, $\stackrel{\sim }{K}\left(t\right)\triangleq K\left(t\right)-K^{\ast }$, $\stackrel{\sim }{L}\left(t\right)\triangleq L\left(t\right)-L^{\ast }$, ${\stackrel{\sim }{K}}_f\left(t\right)=K_f\left(t\right)-K^{\ast }$, and ${\stackrel{\sim }{L}}_f\left(t\right)=L_f\left(t\right)-L^{\ast }$ are the parametric errors. The resulting dynamics for the parametric errors based on the $\sigma$-modification of MRAC’s adaptive laws with low-pass filter estimation are given as:

$$\begin{array}{c}\dot{e}\left(t\right)=A_{m}e+B_m{L^{\ast }}^{-1}\left(-\stackrel{\sim }{K}y+\stackrel{\sim }{L}r\right)+d\left(t\right),e\left(0\right)=e_0\\ \dot{\stackrel{\sim }{K}}\left(t\right)=\mathrm{\Lambda }\left(B_m^T\stackrel{\sim }{P}e{y}^T-\sigma \left(\stackrel{\sim }{K}-{\stackrel{\sim }{K}}_f\right)\right),\stackrel{\sim }{K}\left(0\right)={\stackrel{\sim }{K}}_0\\ \begin{array}{c}\dot{\stackrel{\sim }{L}}\left(t\right)=\mathrm{\Lambda }\left(-B_m^T\stackrel{\sim }{P}e{r}^T-\sigma \left(\stackrel{\sim }{L}-{\stackrel{\sim }{L}}_f\right)\right),\stackrel{\sim }{L}\left(0\right)={\stackrel{\sim }{L}}_0\\ \begin{array}{c}{\dot{\stackrel{\sim }{K}}}_f\left(t\right)=\lambda \left(\stackrel{\sim }{K}-{\stackrel{\sim }{K}}_f\right),{\stackrel{\sim }{K}}_f\left(0\right)={\stackrel{\sim }{K}}_0\\ {\dot{\stackrel{\sim }{L}}}_f\left(t\right)=\lambda \left(\stackrel{\sim }{L}-{\stackrel{\sim }{L}}_f\right),{\stackrel{\sim }{L}}_f\left(0\right)={\stackrel{\sim }{L}}_0\end{array}\end{array}\end{array}$$E14

Theorem:Consider the plant dynamics shown inEq. (1), the reference model inEq. (2), the control law inEq. (5). Then, the solution$\left(e\left(t\right),\stackrel{\sim }{K}\left(t\right),\stackrel{\sim }{L}\left(t\right),{\stackrel{\sim }{K}}_f\left(t\right),{\stackrel{\sim }{L}}_f\left(t\right)\right)$of the dynamical system given byEq. (14)is uniformly bounded for all$\left(e_0,{\stackrel{\sim }{K}}_0,{\stackrel{\sim }{L}}_0,{\stackrel{\sim }{K}}_{f0},{\stackrel{\sim }{L}}_{f0}\right)\in D_{\alpha }$where$D_{\alpha }$is a compact positive invariant set, with ultimate bound.

$${‖e\left(t\right)‖}_2<2\frac{{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)d_{\mathit{max}}}{{\lambda }_{\mathit{min}}\left(Q\right)},t\ge 0$$E15

Additionally, the L₂ – norm of error is bounded from above for $\mathrm{t}\ge 0$ as indicated below:

$${‖e‖}_{L_2}^2\le \frac{1}{\left|{\lambda }_{\mathit{min}}\left(Q\right)-{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\right|}\left(V_0+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)d_{\mathit{max}}^2\right).$$E16

Proof: We consider the following Lyapunov candidate function:

$$V\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)=e^T\stackrel{\sim }{P}e+\mathit{tr}\left({\stackrel{\sim }{K}}^T\mathrm{\Gamma }{\mathrm{\Lambda }}^{-1}\stackrel{\sim }{K}\right)+\mathit{tr}\left({\stackrel{\sim }{L}}^T\mathrm{\Gamma }{\mathrm{\Lambda }}^{-1}\stackrel{\sim }{L}\right)+\frac{\sigma }{\lambda }\mathit{tr}\left({\stackrel{\sim }{K}}_f^T\mathrm{\Gamma }{\stackrel{\sim }{K}}_f\right)+\frac{\sigma }{\lambda }\mathit{tr}\left({\stackrel{\sim }{L}}_f^T\mathrm{\Gamma }{\stackrel{\sim }{L}}_f\right)$$E17

where $\stackrel{\sim }{P}={\stackrel{\sim }{P}}^T>0$ satisfies the Lyapunov equation in Eq. (7). Since $\stackrel{\sim }{P},\mathrm{\Gamma },\mathrm{\Lambda }$ are positive definite, $\sigma >0$, and $\lambda >0$; $V\left(0,0,0,0,0\right)=0$ and $V\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)>0$ for all $\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)\ne \left(0,0,0,0,0\right)$. Also, $V\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)$ is radially unbounded. The time derivative along system trajectories is

$$\dot{V}={\dot{e}}^T\stackrel{\sim }{P}e+e^T\stackrel{\sim }{P}\dot{e}+2\mathit{tr}\left({\stackrel{\sim }{K}}^T\mathrm{\Gamma }{\mathrm{\Lambda }}^{-1}\dot{\stackrel{\sim }{K}}\right)+2\mathit{tr}\left({\stackrel{\sim }{L}}^T\mathrm{\Gamma }{\mathrm{\Lambda }}^{-1}\dot{\stackrel{\sim }{L}}\right)+2\frac{\sigma }{\lambda }\mathit{tr}\left({\stackrel{\sim }{K}}_f^T\mathrm{\Gamma }\dot{{\stackrel{\sim }{K}}_f}\right)+2\frac{\sigma }{\lambda }\mathit{tr}\left({\stackrel{\sim }{L}}_f^T\mathrm{\Gamma }\dot{{\stackrel{\sim }{L}}_f}\right)$$E18

From the error dynamics shown in Eq. (14), we can simplify it as:

$$\dot{V}=\begin{array}{l}{e}^T\left(A_m^T\stackrel{\sim }{P}+\stackrel{\sim }{P}{A}_m\right)e+2e^T\stackrel{\sim }{P}{B}_m{L}^{\ast -1}\left(-\stackrel{\sim }{K}y+\stackrel{\sim }{L}r\right)+2\mathit{tr}\left({\stackrel{\sim }{K}}^T\mathrm{\Gamma }{\mathrm{\Lambda }}^{-1}\dot{\stackrel{\sim }{K}}\right)\\ +2\mathit{tr}\left({\stackrel{\sim }{L}}^T\mathrm{\Gamma }{\mathrm{\Lambda }}^{-1}\dot{\stackrel{\sim }{L}}\right)+2\frac{\sigma }{\lambda }\mathit{tr}\left({\stackrel{\sim }{K}}_f^T\mathrm{\Gamma }\dot{{\stackrel{\sim }{K}}_f}\right)+2\frac{\sigma }{\lambda }\mathit{tr}\left({\stackrel{\sim }{L}}_f^T\mathrm{\Gamma }\dot{{\stackrel{\sim }{L}}_f}\right)+2e^T\stackrel{\sim }{P}d\left(t\right)\end{array}$$E19

Using Eqs. (7), (14) and (19) results as:

$$\dot{V}=\begin{array}{l}-e^T\mathit{Qe}-2\mathit{tr}\left[{\stackrel{\sim }{K}}^T\mathrm{\Gamma }\left(\left(B_m^T\stackrel{\sim }{P}e{y}^T-\sigma \left(\stackrel{\sim }{K}-{\stackrel{\sim }{K}}_f\right)\right)-{\mathrm{\Lambda }}^{-1}\dot{\stackrel{\sim }{K}}\right)\right]\\ +2\mathit{tr}\left[{\stackrel{\sim }{L}}^T\mathrm{\Gamma }\left(\left(B_m^T\stackrel{\sim }{P}e{r}^T+\sigma \left(\stackrel{\sim }{L}-{\stackrel{\sim }{L}}_f\right)\right)+{\mathrm{\Lambda }}^{-1}\dot{\stackrel{\sim }{L}}\right)\right]+2e^T\stackrel{\sim }{P}d\left(t\right)\end{array}$$E20

for some arbitrary $Q=Q^T>0$ in the Lyapunov equation.

Therefore, for the adaptive laws shown in Eq. (13), we have

$$\begin{array}{rcl}\dot{V}\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)& =& -e^T\mathit{Qe}+2e^T\stackrel{\sim }{P}d\left(t\right)\le -{\lambda }_{\mathit{min}}\left(Q\right){‖e‖}^2+2‖e‖{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)d_{\mathit{max}}\\ & \le & -{\lambda }_{\mathit{min}}\left(Q\right)‖e‖\left(‖e‖-2\frac{{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)}{{\lambda }_{\mathit{min}}\left(Q\right)}{d}_{\mathit{max}}\right)\end{array}$$E21

Consequently, the $\dot{V}<0$outside of the compact set given below:

$$E_0=\left\{\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right):\Vert e\Vert \le 2\frac{{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)}{{\lambda }_{\mathit{min}}\left(Q\right)}{d}_{\mathit{max}}=e_0\right\}$$E22

The system trajectory $\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right).$ starts outside the compact set, $E_0$ will reach the boundary of a compact set in a finite time and will remain there. Hence, $e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\in L_{\infty }$

To find the L₂-norm of tracking error, we start with Eq. (21)

$$\dot{V}\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)=e^T\mathit{Qe}+2e^T\stackrel{\sim }{P}d\left(t\right)\le -{\lambda }_{\mathit{min}}\left(Q\right){‖e‖}^2+2{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\Vert e\Vert \Vert d\Vert$$E23

Using inequality regarding the completion of squares $2\Vert e\Vert \Vert d\Vert \le {‖e‖}^2+{‖d‖}^2$, we write Eq. (23) as:

$$\dot{V}\left(e,\stackrel{\sim }{K},\stackrel{\sim }{L},{\stackrel{\sim }{K}}_f,{\stackrel{\sim }{L}}_f\right)\le \left(-{\lambda }_{\mathit{min}}\left(Q\right)+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\right){‖e‖}^2+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right){‖d‖}^2$$E24

Now integrating with respect to t and taking the limit as $t\to \infty$ results

$$\underset{t\to \infty }{lim}{\int }_0^t\dot{V}\mathit{d\tau }\le \left|-{\lambda }_{\mathit{min}}\left(Q\right)+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\right|\underset{t\to \infty }{lim}{\int }_0^t{‖e‖}^2\mathit{d\tau }+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\underset{t\to \infty }{lim}{\int }_0^t{‖d‖}^2\mathit{d\tau }$$E25

As we know

$$\begin{array}{rcl}-{\int }_0^t\dot{V}\mathit{d\tau }& =& V\left(e_0,{\stackrel{\sim }{K}}_0,{\stackrel{\sim }{L}}_0,{\stackrel{\sim }{K}}_{f0},{\stackrel{\sim }{L}}_{f0}\right)-V\left(e\left(t\right),\stackrel{\sim }{K}\left(t\right),\stackrel{\sim }{L}\left(t\right),{\stackrel{\sim }{K}}_f\left(t\right),{\stackrel{\sim }{L}}_f\left(t\right)\right)\\ & \le & V\left(e_0,{\stackrel{\sim }{K}}_0,{\stackrel{\sim }{L}}_0,{\stackrel{\sim }{K}}_{f0},{\stackrel{\sim }{L}}_{f0}\right)\end{array}$$E26

With definition $V_0\equiv V\left(e_0,{\stackrel{\sim }{K}}_0,{\stackrel{\sim }{L}}_0,{\stackrel{\sim }{K}}_{f0},{\stackrel{\sim }{L}}_{f0}\right)$, the Eq. (25) becomes

$$\left|{\lambda }_{\mathit{min}}\left(Q\right)-{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\right|{‖e‖}_{L_2}^2\le V_0+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)d_{\mathit{max}}^2$$E27

Then, L₂-norm of the tracking error is given by

$${‖e‖}_{L_2}^2\le \frac{1}{\left|{\lambda }_{\mathit{min}}\left(Q\right)-{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)\right|}\left(V_0+{\lambda }_{\mathit{max}}\left(\stackrel{\sim }{P}\right)d_{\mathit{max}}^2\right).$$E28

The proof is completed.

Eq. (26) implies that $e\left(t\right)$ is $\left(d_{\mathit{max}}^2\right)$—small in the mean square sense (m.s.s.), that is, $e\left(t\right)\in S\left(d_{\mathit{max}}^2\right)$. Hence, tracking error is in the order of the disturbance only. When the external disturbance vanishes, the asymptotic property of the tracking error is guaranteed with the $\sigma$-modified adaptive laws using low-frequency learning. The performance of the MR-MRAC scheme will be identical to the MRAC if the external disturbances are zero. The inclusion of low-frequency learning in the adaptive laws of MRAC converts a pure integral type MRAC to a proportional-integral type MRAC [2]. The MR-MRAC enables fast learning ability and improves robustness. The time constant (i.e., ${\lambda }^{-1}$) of the low-pass filter needs to be sufficiently large enough to cut off the high-frequency oscillation [3]. In other words, $\lambda$ needs to be sufficiently small. However, with very small values of $\lambda$, the gains $K\left(t\right),L\left(t\right)$ take a longer time to reach their steady-state values.

Figure 2 presents the schematics of the resulting MR-MRAC architecture Eq. (28). For the given reference input signal $r\left(t\right)$, the tracking error $e\left(t\right)\triangleq y\left(t\right)-y_m\left(t\right)$ is calculated using the plant output $y\left(t\right)$ and the reference model output $y_m\left(t\right)$. This tracking error is used in the $\sigma$-modified adaptive laws. The low-pass filter matrices $K_f\left(t\right)$ and $L_f\left(t\right)$ in the $\sigma$-modified adaptive laws are estimated from the low-frequency learning loop. The estimates of gain matrices $K\left(t\right)$ and $L\left(t\right)$ from the $\sigma$-modified adaptive laws are used in the controller to calculate control input array $u\left(t\right)$. This input array $u\left(t\right)$ is supplied to the APSP.

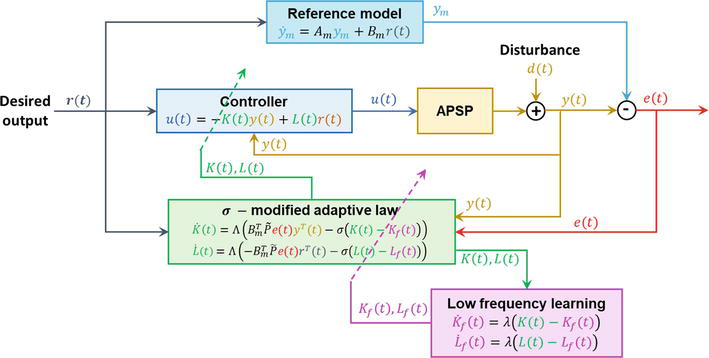
Figure 2.

Schematic of the MR-MRAC architecture [14].

4. Case studies

Shang et al. [8], among others, have provided a mathematical model for the APSP and the associated numerical model. We use LAVA-P software developed at the Idaho National Engineering and Environmental Laboratory to analyze the three-dimensional motions of powder particles within the plasma. Figure 3 depicts the schematic of the proposed robust adaptive process control using the MR-MRAC for generating consistent quality ceramic coating using a single torch—single injection APSP system. Limits on the input variables with symbols indicated in parentheses are Ar flow rate ($P$), 20 slm $\le P$$\le$ 60 slm (standard liters per minute); H₂ flow rate ($Q$), 0 $\le Q$$\le$ 20 slm; and current ($I$), 300 A $\le I$$\le$ 600 A. The effect of disturbances is desired to die out within 50 ms of their occurrence. The sampling time of these simulations is 0.01 ms. The mean values of particles’ axial velocity and temperature are computed in the 1-cm-wide window, 9.5 $\le y\le$10.5 cm located along the jet axis from the nozzle exit.

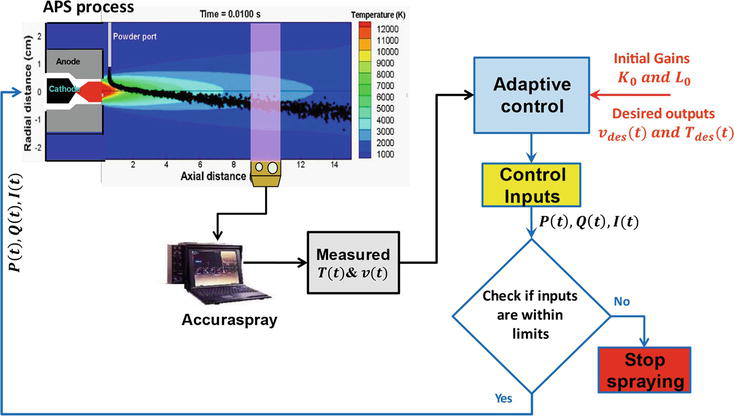
Figure 3.

Schematic of the proposed robust adaptive control scheme for an APSP [13].

Linearizing the nonlinear dynamics of the mean axial velocity $v\left(t\right)$ and the mean temperature $T\left(t\right)$ around an equilibrium point results in the following multi-inputs and multi-outputs (MIMO) SS model:

$$\begin{array}{cc}\left\{\begin{array}{c}\dot{v}\left(t\right)\\ \dot{T}\left(t\right)\end{array}\right\}=\left[\begin{array}{cc}{a}_v& 0\\ 0& a_T\end{array}\right]\left\{\begin{array}{c}v\left(t\right)\\ T\left(t\right)\end{array}\right\}+\left[\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\end{array}\right]\left\{\begin{array}{c}P\left(t\right)\\ Q\left(t\right)\\ I\left(t\right)\end{array}\right\}+\left\{\begin{array}{c}{d}_v\left(t\right)\\ d_T\left(t\right)\end{array}\right\},& \left\{\begin{array}{c}v\left(0\right)=v_0\\ T\left(0\right)=T_0\end{array}\right\}\end{array}$$E29

where $d_v\left(t\right)$ and $d_T\left(t\right)$ are unknown smooth disturbances satisfying ${‖d_v\left(t\right)‖}_2\le d_{v,\mathit{max}},{‖d_T\left(t\right)‖}_2\le d_{T,\mathit{max}},{‖{\dot{d}}_v\left(t\right)‖}_2\le {\dot{d}}_{v,\mathit{max}},{‖{\dot{d}}_T\left(t\right)‖}_2\le {\dot{d}}_{T,\mathit{max}}$ with positive bounds $d_{v,\mathit{max}},d_{T,\mathit{max}},{\dot{d}}_{v,\mathit{max}}\text{and}{\dot{d}}_{T,\mathit{max}}$. Here, the parameters $a_v,a_T,b_{11},\dots ,b_{23}$ are assumed as constants and are dependent on the equilibrium point. The reference model for the MR-MRAC is considered as follows:

$$\begin{array}{cc}\left\{\begin{array}{c}\dot{v_m}\left(t\right)\\ \dot{T_m}\left(t\right)\end{array}\right\}=\left[\begin{array}{cc}-0.5& 0\\ 0& -0.5\end{array}\right]\left\{\begin{array}{c}{v}_m\left(t\right)\\ T_m\left(t\right)\end{array}\right\}+\left[\begin{array}{ccc}0.5& 0& 0.5\\ 0& 0.5& 0.5\end{array}\right]\left\{\begin{array}{c}{v}_{\mathit{des}}\left(t\right)\\ T_{\mathit{des}}\left(t\right)\\ 0\end{array}\right\},& \left\{\begin{array}{c}{v}_m\left(0\right)=v_0\\ T_m\left(0\right)=T_0\end{array}\right\}\end{array}$$E30

We choose $\stackrel{\sim }{P}=I_{2\times 2}$ and $l=1$ in Eq. (13).

The objective is to force the measured MPSs $v\left(t\right)$ and $T\left(t\right)$ from the LAVA-P to track the reference outputs $v_m\left(t\right)$ and $T_m\left(t\right)$ and to convergence to $v_{\mathit{des}}\left(t\right)$ and $T_{\mathit{des}}\left(t\right)$, respectively, within a small bound and within the settling time = 50 ms despite changes in the noise variables. The controller adjusts inputs, such as the argon flow rate $P\left(t\right)$, the hydrogen flow rate $Q\left(t\right)$, and the current $I\left(t\right)$ using control law in Eq. (5), $\sigma$-modified adaptive laws in Eq. (13), and low-pass filter in Eq. (10). From Ref. [18], we choose the following initial gains in Eqs. (10) and (13):

$$\begin{array}{cc}{K}_0=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\end{array}\right];& L_0=\left[\begin{array}{ccc}0.0004& 0.0123& 0\\ 0.0001& 0.0031& 0\\ 0.0045& 0.1430& 0\end{array}\right]\end{array}.$$E31

4.1 Performance comparison of MRAC, R-MRAC, and MR-MRAC

For this study, we use the following adaptive gain matrix in Eq. (13):

$$\mathrm{\Lambda }=\gamma \times \left[\begin{array}{ccc}{10}^{-8}& 0& 0\\ 0& {10}^{-10}& 0\\ 0& 0& {10}^{-9}\end{array}\right]$$E32

where $\gamma$ is the adaptive constant introduced as tuning parameters to achieve the desired transient responses. First, the effect of the adaptive constant $\gamma$ of the standard MRAC (i.e., MR-MRAC with $\sigma =0$ and $\lambda =0$) is investigated using arbitrarily chosen values of $\gamma$ as 1, 5, and 20 in Eq. (32) under the step variation of average injection velocity. The variations of this disturbance and the corresponding control responses are presented in the first column of Figure 4. While the larger values of $\gamma$ speed up the adaption rate for each input; however, it resulted in high-frequency oscillations in control responses, and the performance of the MRAC became unstable. The smaller value of $\gamma$ limits the convergence rate of the plant responses; thus, it takes a longer time to reach the desired values. For $\gamma =5,$ the mean particles’ states have reached the desired values within a settling time of 50 ms with a few minor oscillations in the control responses.

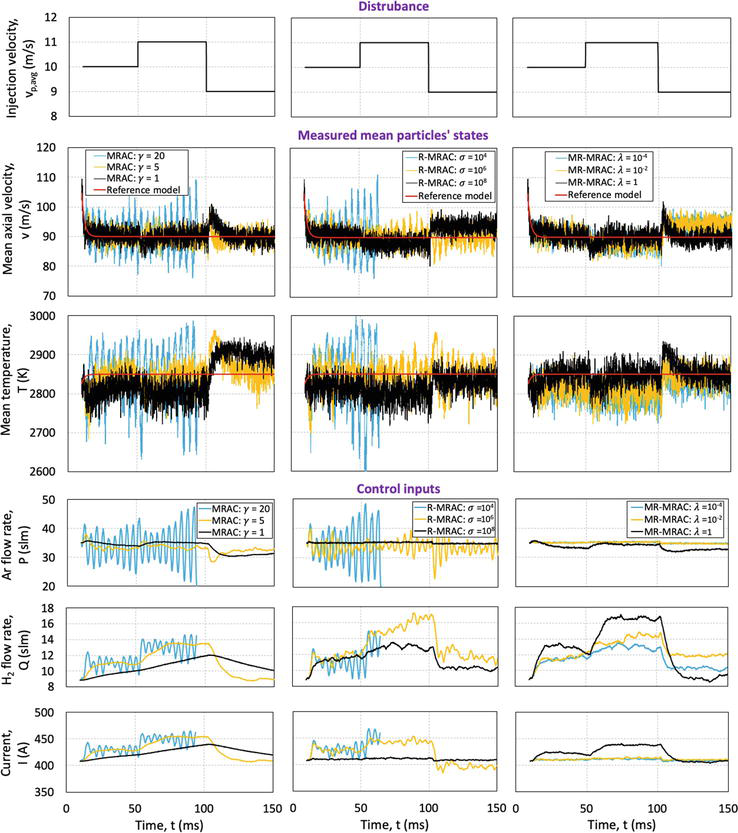
Figure 4.

Effect of adaptive constant $\gamma$ in MRAC (first column), damping constant $\sigma$ in RMRAC (second column for $\gamma =20$), and filter constant $\lambda$ in MR-MRAC (third column for $\gamma =20$ and $\sigma ={10}^8$).

The second column of Figure 4 depicts the effect of damping parameter $\sigma$ in the R-MRAC (i.e., MR-MRAC with $\lambda =0$) for $\sigma$ = 10⁴, 10⁶, and 10⁸. To investigate the fast adaption capability of the proposed controller, the high adaptive constant $\gamma =20$ is considered for this exercise. If the damping parameter $\sigma$ increases from 10⁴ to 10⁶, the frequency of oscillations in the control responses is reduced; however, the steady-state error between the desired and the measured mean particles’ states is increased. For $\sigma ={10}^8,$ the effect of damping is very high, and this leads to an undesirable steady-state error between the measured and desired outputs.

The performance of the MR-MRAC is investigated for $\gamma =20$ and $\sigma ={10}^8$ with the filter constants $\lambda ={10}^{-4}$, $\lambda ={10}^{-2}$, and $\lambda =1$. The fast adaption using a high-gain learning rate is achieved with the MR-MRAC scheme for $\lambda =1$. From the third column of Figure 4, we can observe that the high-frequency oscillations with $\gamma =20$ and steady-state error for $\sigma ={10}^8$ have been reduced with MR-MRAC and the effect of disturbance is attenuated within 20 milliseconds. The smooth variations in the mean particles’ states and control inputs are acquired. This illustrates the point that the designed MR-MRAC achieves the fast and robust adaption without creating highfrequency oscillations or steady-state errors. Therefore, the performance of the MR-MRAC is superior compared to that of the standard MRAC.

4.2 Effect of disturbance variations on performance of MR-MRAC

First, we now check the performance of the MR-MRAC for adaptive tracking when the desired values of mean particles’ states vary with time in the presence of a variation of the disturbance. The following adaptive gain matrix is used for the rest of the analyses:

$$\Lambda =\left[\begin{array}{ccc}2\times {10}^{-8}& 0& 0\\ 0& 2\times {10}^{-10}& 0\\ 0& 0& 5\times {10}^{-9}\end{array}\right]$$E33

Here, the damping constant $\sigma ={10}^8$ and the filter constant $\lambda =1$. In this case, the performances of the MRAC and the MR-MRAC are compared, and the subsequent results are presented in Figure 5 for step variations in $v_{\mathit{des}}\left(t\right)\mathit{\text{and}}{T}_{\mathit{des}}\left(t\right)$ in the presence of the step variation of average particles’ injection velocity. It is evident that both controllers effectively force the mean particles’ states to follow the outputs of the reference model despite larger magnitudes of the error between the measured and the desired particles’ states. However, the magnitude of the mean temperature oscillations is significantly dampened using the MR-MRAC. Even if the mean particles’ states reach the desired values faster than the MR-MRAC in this particle case, faster convergence can be achieved for MR-MRAC by further fine-tuning of the filter constant $\lambda$.

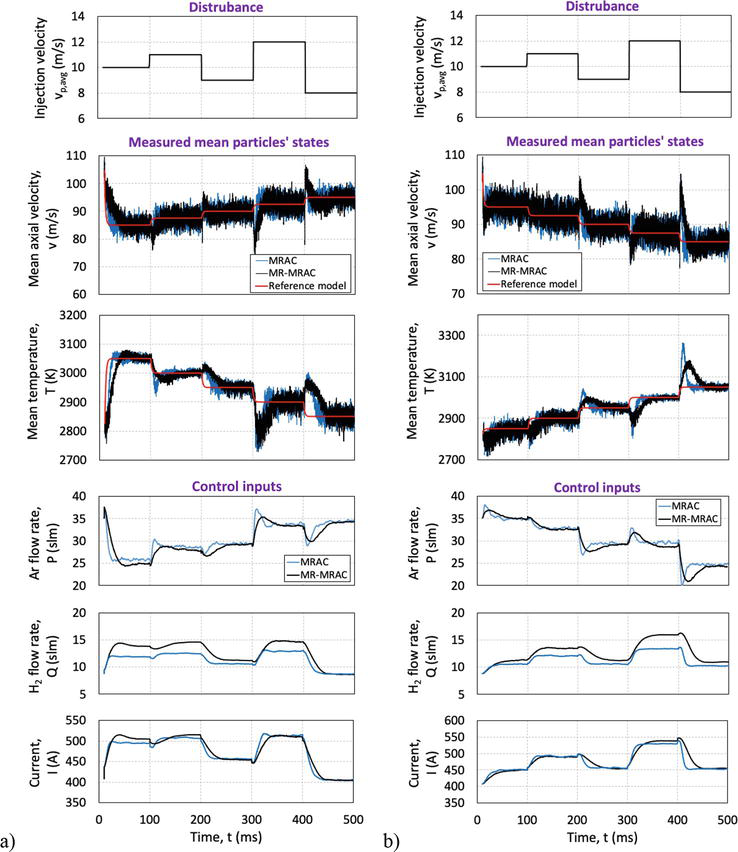
Figure 5.

The closed-loop control responses of MRAC and MR-MRAC for a) increasing desired mean particles’ axial velocity and decreasing desired mean particles’ temperature; and b) the decreasing desired mean particles’ axial velocity but increasing desired mean particles’ temperature in the presence of step disturbance in average injection velocity.

The effect of the simultaneously varied disturbances, such as the average injection velocity of particles and the arc voltages (in the first and the second row of Figure 6), on the mean axial velocity and mean temperature are shown in the third and the fourth rows of Figure 6, respectively. The performance of the MR-MRAC is investigated under these disturbances, and the varied control outputs are shown in the fifth and the sixth rows of Figure 6, and the corresponding control inputs are presented in the remaining rows of Figure 6. These examples establish the effectiveness of the designed process controller in mitigating the effects of various classes of disturbances for generating ceramic coatings using the APSP. Of course, in practice, disturbances are not limited to those stipulated here.

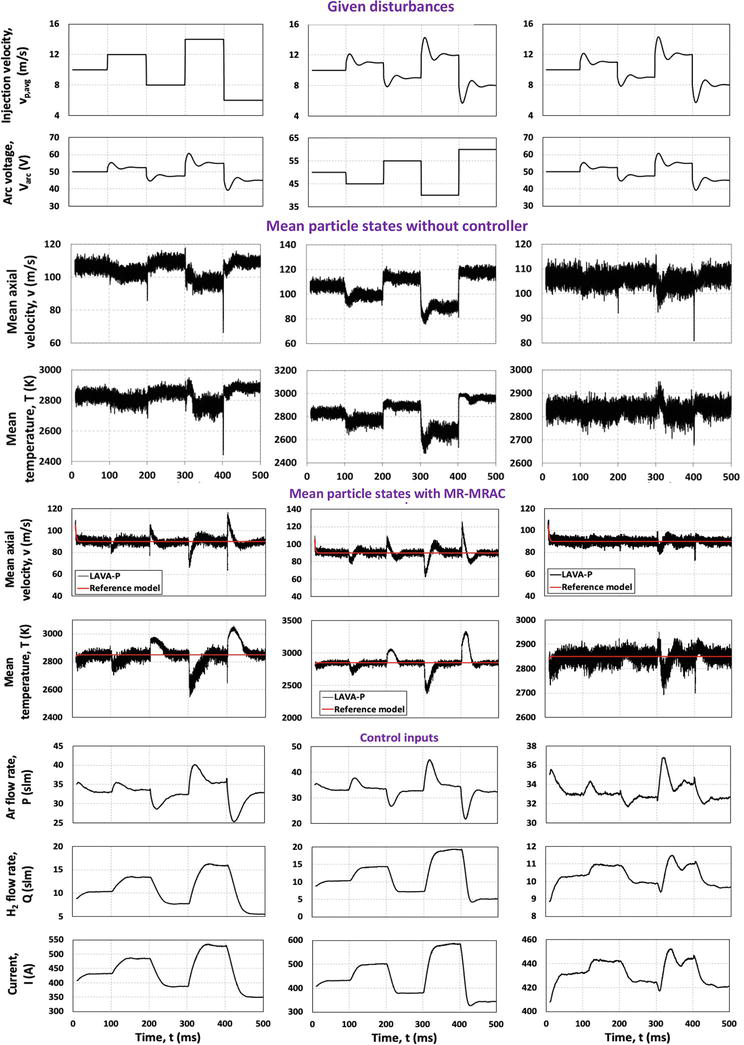
Figure 6.

The closed-loop responses of the MR-MRAC system in the presence of combined disturbances of the average powder injection velocity and the arc voltage.

5. Conclusion

This chapter proposes two modifications to the standard model reference adaptive control (MRAC) to improve the robustness and the fast adaption, and its application to the atmospheric plasma spray process (APSP) to improve repeatability and reproducibility of coating quality and simultaneously decreasing manufacturing costs. The MRAC lacks robustness in the presence of process uncertainties and bounded external disturbances, which is a well-known drawback. This issue is handled by the modified robust MRAC (MR-MRAC) scheme, which consists of sigma-modified adaptive laws of MRAC with a low-pass weight estimated filter. The control objective for the APSP is to get consistency in mean particles’ states, such as mean axial velocity and mean temperature, before impacting the substrate. The performance of this strategy is tested on numerical software LAVA-P simulates the APSP. The MR-MRAC shows better performance compared to standard MRAC under external disturbances. The desired consistency in mean particles’ states is achieved despite artificially induced disturbances by varying control inputs through fast adaption. The smooth variations in the mean particles’ states and control inputs are acquired without generating high-frequency oscillations or steady-state errors.

We anticipate that the MR-MRAC will perform equally well in practical applications and economically enable the production of high-quality coatings. This control architecture also is feasible for other coating methods, such as the HVOF spray process, physical vapor deposition, and chemical vapor deposition.

Conflict of interest

The authors declare that they have no conflict of interest.